Méthode de Newton :
Soit \(f:[a,b]\to{\Bbb R}\) une fonction dérivable
Alors la suite définie par $$u_0\in[a,b]\quad\text{ et }\quad u_{n+1}=u_n-\frac{f(u_n)}{f'(u_n)}$$
Converge vers la solution \(\ell\) de \(f(x)=0\)
(Dérivabilité, Suite réelle, //Méthode de la sécante)
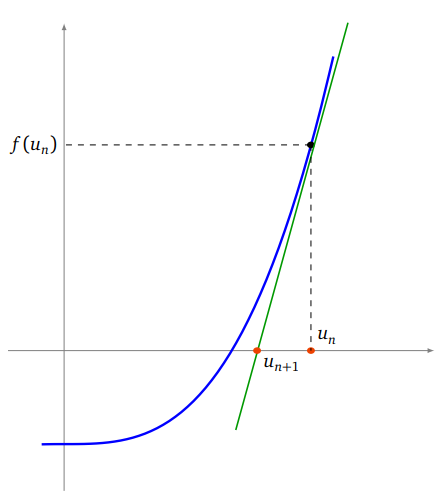
La méthode de Newton a pour avantage de converger très très vite vers la valeurs désirée
Théorème :
Soit \(g\in\mathcal C^2(I,{\Bbb R})\) une fonction admettant un zéro \(\alpha\) dans l'intérieur de \(I\)
On suppose que \(g'(\alpha)\neq0\)
Alors il existe \(\rho\gt 0\) tel que pour tout \(x_0\in]\alpha-\rho,\alpha+\rho[\), la suite de la méthode de Newton est bien définie et converge vers \(\alpha\)
De plus, la convergence est au moins quadratique
(Classe de fonctions, Intérieur, Ordre d’une méthode de quadrature)